
In CNC lathe machines, the parallel direction of the spindle is Z axis. The head direction is negative (-Z), and the direction perpendicular to Z axis is X and Y directions.
You can use the thumb of the left hand (X axis), the index finger (Y axis), and the middle finger (Z axis) to become three axes. The direction indicated by the fingertip is the positive direction of each axis, and the forward direction of the three axes of the machine tool can be easily defined.
Therefore, Z axis is -Z toward the chuck of the lathe, and X axis is moving in the direction of the turret so that the direction in which the workpiece becomes smaller is -X.
In addition to the XYZ three linear axis, there are three other rotating axis and three auxiliary axis.
The three rotating axes are:
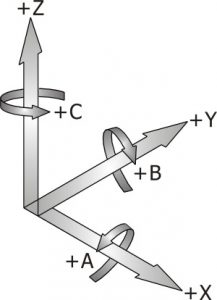
A axis: rotating around X axis
B axis: rotating around Y axis
C axis: rotating around Z axis
The three auxiliary axis are:
U axis: parallel to X axis
V axis: parallel to Y axis
W axis: parallel to Z axis
You can find the photo display of the CNC machining parts made by us HERE!
